Môn Tài chính và quản lý tài chính nâng cao được đánh giá là bộ môn khó nhằn nhất trong kỳ thi CPA. Bởi hàng loạt các khái niệm, công thức tính phức tạp buộc thí sinh cần ghi nhớ và hiểu đúng mới có thể hoàn thành các bài tập trong đề thi.
Để các bạn ôn thi CPA dễ dàng, bài viết này VisioEdu sẽ giúp bạn hiểu rõ hơn về khái niệm “Giá trị hiện tại của tiền” và công thức tính giá trị hiện tại của một khoản tiền.
1. Giá trị hiện tại của tiền khi thi CPA là gì?
Có thể bạn đã biết, tiền luôn luôn có giá trị theo thời gian, vì 1 đồng mà ta nhận được ở thời điểm ngày hôm nay thường có giá trị hơn 1 đồng nhận được ở một thời điểm nào đó trong tương lai.
VisioEdu nhận thấy, tiền có giá trị theo thời gian bởi 3 nguyên nhân cơ bản sau:
– Do cơ hội sử dụng tiền : Đồng tiền ở hiện tại có thể được đầu tư để sinh lời, do đó, tiền phải tạo ra tiền lớn hơn.
– Do lạm phát : Cùng với thời gian, lạm phát có thể xảy ra. Trong môi trường có lạm phát, đồng tiền sẽ bị mất giá, sức mua của tiền giảm theo thời gian, làm cho một đồng tiền nhận được trong tương lai có giá trị thấp hơn một đồng tiền nhận được ngày hôm nay.
– Rủi ro, sự không chắc chắn : Tương lai lúc nào cũng bao hàm một ý niệm không chắc chắn, do đó, một đồng nhận được trong tương lai không thể có cùng giá trị với một đồng nhận được ngày hôm nay.

2. Giá trị hiện tại của một khoản tiền
Để bạn hiểu rõ hơn, tiếp theo, VisioEdu sẽ giới thiệu đến bạn khái niệm giá trị hiện tại của một khoản tiền và công thức xác định giá trị hiện tại của một khoản tiền khi ôn thi CPA môn Tài chính và quản lý tài chính nâng cao.
2.1 Khái niệm
Giá trị hiện tại của một khoản tiền (còn gọi là hiện giá) là giá trị của khoản tiền phát sinh trong tương lai được quy về thời điểm hiện tại (thời đỉểm gốc) theo một tỷ lệ chiết khấu nhất định.
Như trên đã nêu, lãi suất được coi là giá trị của thời gian và rủi ro. Vì thế, để tính đổi giá trị của một khoản tiền trong tương lai về giá trị hiện tại, người ta phải sử dụng một lãi suất như một công cụ để chiết khấu giá trị theo thời gian.
Để bạn hiểu sâu hơn về giá trị thời gian của tiền khi ôn thi CPA môn Tài chính và quản lý tài chính nâng cao, hãy cùng VisioEdu phân tích 1 ví dụ cụ thể sau:
Một người hiện có 100 triệu đồng và đem cho vay với lãi suất 10%/năm, như vậy sau 1 năm người đó có số tiền là 100 x (l + 10%) = 110 triệu đồng. Điều đó cũng có nghĩa là giá trị hiện tại của khoản tiền 110 triệu đồng là 100 triệu đồng. Vậy nếu sau 1 năm sẽ thu được số tiền là 110 triệu đồng thì giá trị hiện tại của nó sẽ được tính là triệu đồng.
Video bài giảng Ôn thi CPA 2023 môn Tài chính và quản lý tài chính nâng cao của VisioEdu.
2.2 Công thức tính giá trị hiện tại của 1 khoản tiền
Công thức tổng quát xác định giá trị hiện tại của một khoản tiền như sau:
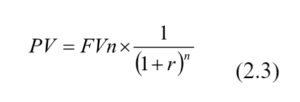
Trong đó:
PV: Giá trị hiện tại của khoản gtiền phát sinh trong tương lai
FVn: Giá trị khoản tiền tại thời điểm cuối kỳ n trong tương lai
r: Tỷ lệ chiết khấu hay tỷ lệ hiện tại hóa
n: Số kỳ chiết khấu
được gọi là hệ số chiết khấu hay hệ số hiện tại hóa, nó biểu thị giá trị hiện tại của 1 đồng phát sinh ở cuối kỳ thứ n trong tương lai và được ký hiệu là p(r,n). Từ đó công thức tính giá trị hiện tại của 1 khoản tiền trong tương lai ở trên có thể viết dưới dạng sau:
PV = FVn x p(r,n)
Có thể sử dụng bảng tra bảng phụ lục số 2 để xác định giá trị hiện tại của một đồng với các giá trị tương ứng r và n
Như vậy, thực chất của cách tính giá trị hiện tại là phép tính ngược của cách tính giá trị tương lai. Phương pháp tính như trên được gọi là phương pháp hiện tại hóa giá trị hay phương pháp chiết khấu giá trị.
Xem xét công thức tính giá trị hiện tại của một khoản tiền nêu trên có thể rút ra nhận xét:
– Thời điểm phát sinh khoản tiền càng xa thời điểm hiện tại thì giá trị hiện tại của khoản tiền càng nhỏ.
– Tỷ lệ chiết khấu hay tỷ lệ hiện tại hóa càng lớn thì giá trị hiện tại của khoản tiền càng nhỏ.
Cùng VisioEdu phân tích một ví dụ cụ thể sau để hiểu rõ hơn về giá trị hiện tại của một khoản tiền và ứng dụng công thức tính khi giải bài thi CPA nhé!
Một người muốn để dành tiền cho con đi du học bằng cách gửi tiết kiệm vào một ngân hàng, lãi suất ngân hàng ổn định mức 5%/năm, kỳ hạn ghép lãi mỗi năm một lần. Người đó muốn có số tiền là 50.000 USD sau 10 năm nữa thì ngay bây giờ phải gửi vào ngân hàng là bao nhiêu?
Ta có: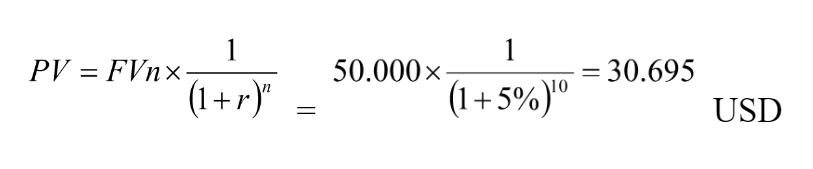
Hay: PV = FVnx p(r,n) = 50.000 x 0,6139 = 30.695 USD
Trên đây là toàn bộ nội dung quan trọng liên quan đến giá trị hiện tại của một khoản tiền và công thức tính. Nếu bạn muốn vượt qua kỳ thi CPA dễ dàng ở môn Tài chính và quản lý tài chính nâng cao, hãy ghi nhớ công thức tính giá trị thời gian của một khoản tiền mà VisioEdu chia sẻ bên trên nhé.
Nếu trong quá trình ôn thi CPA bạn gặp khó khăn gì, đừng ngần ngại chia sẻ cho chúng tôi để được hỗ trợ nhé!

















